Introduction
In this chapter we will have the introduction, definition of statistics, collection and classification of data, formation of frequency distribution.(Goon and Dasgupta 1983) (Gupta and Kapoor 1997)
Origin of the word “Statistics”
Term statistics was derived from the Neo-Latin word
statisticum collegium meaning “council of state” and the Italian word
statista meaning “statesman” or “politician”.
A German word Statistik, got the meaning “collection and
classification of data” generally in the early 19th century. This word
was first introduced by Gottfried Achenwall (1749). Statistik was
originally designated as a term for analysis of data about the state
(data used by government or other administrative bodies). The term
Statistik was introduced into English in 1791 by Sir John Sinclair
when he published the first of 21 volumes titled “Statistical Account of
Scotland” (Ball 2004). The first book to have ‘Statistics’ in its title was
“Contributions to Vital Statistics” (1845) by Francis GP Neison,
actuary to the Medical Invalid and General Life Office.
Statistics and Mathematics
Mathematics follows a rigid theorem and proof. Mathematical theories
involve well-defined and proven facts which has the minimal scope of
change. However, Statistics is a discipline where real-life data is
handled. This factor makes this field of study more abstract, where
individuals have to develop newer solutions to problems that was new and
not observed before. Statistics is an applied science; in mathematics
the goal is to prove theorems. In statistics, the main goal is to
develop good methods for understanding data and making decisions.
Statisticians often use mathematical theorems to justify their methods,
but theorems are not the main focus. Statistics is now considered as an
independent field which uses mathematics to solve real life problems.
Definition of Statistics
Statistics is the science which deals with the
Two main branches of statistics are:
Descriptive statistics, which deals with summarizing data from a
sample using indexes such as the mean or standard deviation etc.
Inferential statistics, use a random sample of data taken from a
population to describe and make inferences about the population
parameters.
Data
Data can be defined as individual pieces of factual information recorded
and used for the purpose of analysis. It is the raw information from
which inferences are drawn using the science “STATISTICS”.
Example for data
No. of farmers in a village.
The rainfall over a period of time.
Area under paddy crop in a state.
Use and limitations of statistics
Functions of statistics: Statistics simplifies complexity, presents
facts in a definite form, helps in formulation of suitable policies,
facilitates comparison and helps in forecasting. Valid results and
conclusion are obtained in research experiments using proper statistical
tools.
Uses of statistics: Statistics has pervaded almost all spheres of
human activities. Statistics is useful in the administration, industry,
business, economics, research workers, banking,insurance companies etc.
Limitations of Statistics
Statistical theories can be applied only when there is variability
in the experimental material.
Statistics deals with only aggregates or groups and not with
individual objects.
Statistical results are not exact.
Statistics are often misused.
Population and Sample
Consider the following example. Suppose we wish to study the height of
all students in a college. It will take us a long time to measure the
height of all students of the college and so we may select 20 of the
students and measure their height (in cm). Suppose we obtain the
measurements like this
149 156 148 161 159 143 158 152 164 171 157 152 163 158 151 147 157 146
153 159
In this study, we are interested in the height of all students in the
college. The set of height of all students in the college is called the
population of this study. The set of 20 height, H = {149, 156,148,
…, 153, 159}, is a sample from this population.
Population
A population is the set of all objects we wish to study
Sample
A sample is part of the population we study to learn about the
population.
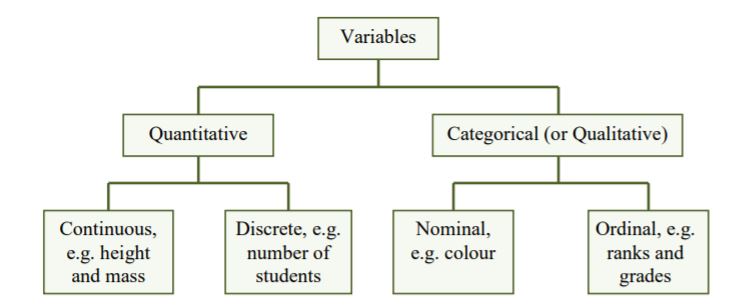
Variables and constants
Variables
Any type of observation which can take different values for different
people, or different values at different times, or places, is called a
variable. The following are examples of variables:
number of fruits in a branch, number of plots in a field, number of
schools in a country, etc.
plant height, yield, panicle length, temperature,etc.
Broadly speaking, there are two types of variables – quantitative
and qualitative (or categorical) variables.
Constants
Constants are characteristics that have values that do not change.
Examples of constants are: pi (𝝅) = the ratio of the circumference of a
circle to its diameter (𝝅 = 3.14159...) and e, the base of the
natural or (Napierian) logarithms (e=2.71828).
Types of variables
Quantitative variables
A quantitative variable is one that can take numerical values. The
variables like number of fruits in a branch, number of plots in a field,
number of schools in a country, plant height, yield, panicle length,
temperature, etc. are examples of quantitative variables. Quantitative
variables may be characterized further as to whether they are discrete
or continuous
Discrete variables
The variables like number of fruits in a branch, number of plots in a
field, number of schools in a country, etc. can be counted. These are
examples of discrete variables. Variables that can only take on a finite
number of values are called “discrete variables.” Any variable phrased
as “the number of …”, is discrete, because it is possible to list its
possible values {0,1, …}. Any variable with a finite number of
possible values is discrete. The following example illustrates the
point. The number of daily admissions to a hospital is a discrete
variable since it can be represented by a whole number, such as 0, 1, 2
or 3. The number of daily admissions on a given day cannot be a number
such as 1.8, 3.96 or 5.33.
Continuous variables
The variables like plant height, yield, panicle length, temperature,
etc. can be measured. These are examples of continuous variables. A
continuous variable does not possess the gaps or interruptions
characteristic of a discrete variable. A continuous variable can assume
any value within a specific relevant interval of values assumed by the
variable. Notice that age is continuous since an individual does not age
in discrete jumps. Panicle length can be measured as 5.5, 5.8 cm etc so,
it is a continuous variable.
Categorical variables
A variable is called categorical when the measurement scale is a set of
categories. For example, marital status, with categories
(single,married, widowed), is categorical. Whether employed (yes, no),
religious affiliation (Protestant, Catholic, Jewish, Muslim, others,
none), colours etc. Categorical variables are often called qualitative.
It can be seen that categorical variables can neither be measured nor
counted.
Measurement scales
Variables can further be classified according to the following four
levels of measurement: nominal, ordinal, interval and ratio.
Nominal scale
This scale of measure applies to qualitative variables only. On the
nominal scale, no order is required. For example,gender is nominal,
blood group is nominal, and marital status is also nominal. We cannot
perform arithmetic operations on data measured on the nominal scale.
Ordinal scale
This scale also applies to qualitative data. On the ordinal scale, order
is necessary. This means that one category is lower than the next one or
vice versa. For example, Grades are ordinal, as excellent is higher than
very good, which in turn is higher than good, and so on. It should be
noted that, in the ordinal scale, differences between category values
have no meaning.
Interval scale
This scale of measurement applies to quantitative data only. In this
scale, the zero point does not indicate a total absence of the quantity
being measured. An example of such a scale is temperature on the Celsius
or Fahrenheit scale. Suppose the minimum temperatures of 3 cities, A, B
and C, on a particular day were 00C, 200C and 100C, respectively.
It is clear that we can find the differences between these temperatures.
For example, city B is 200C hotter than city A. However, we cannot say
that city A has no temperature. Moreover, we cannot say that city B is
twice as hot as city C, just because city B is 200C and city C is
100C. The reason is that, in the interval scale, the ratio between two
numbers is not meaningful.
Ratio scale
This scale of measurement also applies to quantitative data only and has
all the properties of the interval scale. In addition to these
properties, the ratio scale has a meaningful zero starting point and a
meaningful ratio between 2 numbers. An example of variables measured on
the ratio scale, is weight. A weighing scale that reads 0 kg gives an
indication that there is absolutely no weight on it. So the zero
starting point is meaningful. If Ram weighs 60 kg and Laxman weighs 30
kg, then Ram weighs twice as Laxman. Another example of a variable
measured on the ratio scale is temperature measured on the Kelvin scale.
This has a true zero point.
Collection of Data
The first step in any enquiry (investigation) is the collection of data.
The data may be collected for the whole population or for a sample only.
It is mostly collected on a sample basis. Collecting data is very
difficult job. The enumerator or investigator is the well trained
individual who collects the statistical data. The respondents are the
persons from whom the information is collected.
Types of Data
There are two types (sources) for the collection of data:
- Primary Data
- Secondary Data
Primary Data
Primary data are the first hand information which is collected, compiled
and published by organizations for some purpose. They are the most
original data in character and have not undergone any sort of
statistical treatment.
Example: Population census reports are primary data because these are
collected, complied and published by the population census organization.
Secondary Data
The secondary data are the second hand information which is already
collected by an organization for some purpose and are available for the
present study. Secondary data are not pure in character and have
undergone some treatment at least once.
Example: An economic survey of England is secondary data because the
data are collected by more than one organization like the Bureau of
Statistics, Board of Revenue, banks, etc.
Methods of Collecting Primary Data
Primary data are collected using the following methods:
Personal Investigation
The researcher conducts the survey him/herself and collects data from
it. The data collected in this way are usually accurate and reliable.
This method of collecting data is only applicable in case of small
research projects.
Through Investigation
Trained investigators are employed to collect the data. These
investigators contact the individuals and fill in questionnaires after
asking for the required information. Most organizations utilize this
method.
Collection through Questionnaire
Researchers get the data from local representations or agents that are
based upon their own experience. This method is quick but gives only a
rough estimate.
Through the Telephone
Researchers get information from individuals through the telephone. This
method is quick and gives accurate information.
Methods of Collecting Secondary Data
Secondary data are collected by the following methods:
Official
Publications from the Statistical Division, Ministry of Finance, the
Federal Bureaus of Statistics, Ministries of Food, Agriculture,
Industry, Labor, etc.
Semi-Official
- Publications from State Bank, Railway Board, Central Cotton
Committee, Boards of Economic Enquiry etc.
- Publication of Trade Associations, Chambers of Commerce, etc.
- Technical and Trade Journals and Newspapers.
- Research Organizations such as universities and other institutions.
Difference Between Primary and Secondary Data
The difference between primary and secondary data is only a change of
hand. Primary data are the first hand information which is directly
collected form one source. They are the most original in character and
have not undergone any sort of statistical treatment, while secondary
data are obtained from other sources or agencies. They are not pure in
character and have undergone some treatment at least once.
Frequency distribution
Table shows the number of fruits per branch in a mango
tree selected from a particular plot. The data, presented in this form
in which it was collected, is called raw data.
It can be seen that, the minimum and the maximum numbers of fruits per branch are 0 and 5, respectively. Apart from these numbers, it is impossible, without further careful study, to extract any exact information from the data. But by breaking down the data into the form below
Now certain features of the data become apparent. For instance, it can easily be seen that, most of the branches selected have four fruits because number of branches having 4 fruits is 7. This information cannot easily be obtained from the raw data. The above table is called a frequency table or a frequency distribution. It is so called because it gives the frequency or number of times each observation occurs. Thus, by
finding the frequency of each observation, a more intelligible picture is obtained.
Construction of frequency distribution
List all values of the variable in ascending order of magnitude.
Form a tally column, that is, for each value in the data, record a
stroke in the tally column next to that value. In the tally, each
fifth stroke is made across the first four. This makes it easy to
count the entries and enter the frequency of each observation.
Check that the frequencies sum to the total number of observations
Grouped frequency distribution
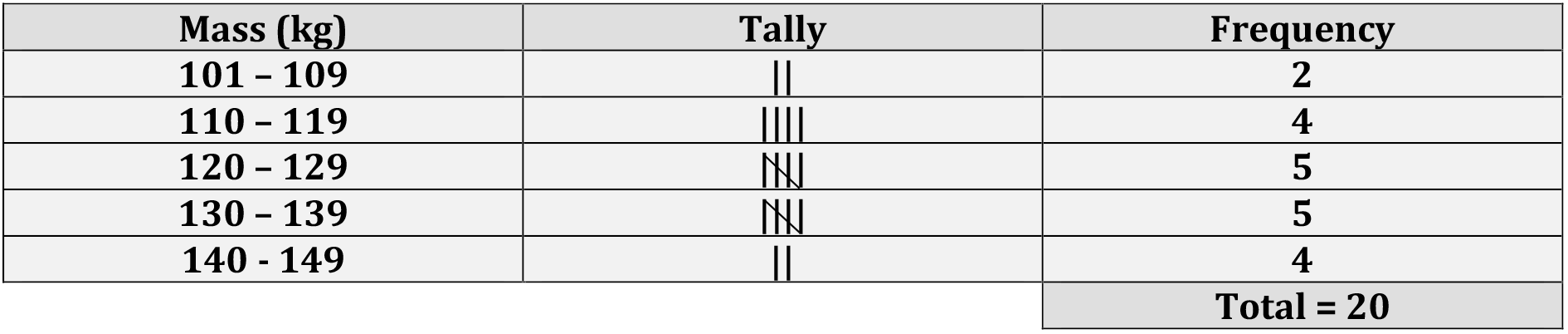
Data below gives the plant height of 20 paddy varieties, measured to the
nearest centimeters.
It can be seen that the minimum and the maximum plant height are 107 cm
and 144 cm, respectively. A frequency distribution giving every plant height between 107 cm and 144 cm would be very long and would not be very
informative. The problem is to overcome by grouping the data into
classes.
If we choose the classes
100 – 109
110 – 119
120 – 129
130 – 139
140 – 149
we obtain the frequency distribution given below:
Above table gives the frequency of each group or class; it is therefore
called a grouped frequency table or a grouped frequency distribution.
Using this grouped frequency distribution, it is easier to obtain
information about the data than using the raw data. For instance, it can
be seen that 14 of the 20 paddy varieties have plant height between 110
cm and 139 cm (both inclusive). This information cannot easily be
obtained from the raw data.
It should be noted that, even though above table is concise, some
information is lost. For example, the grouped frequency distribution
does not give us the exact plant height of the paddy varieties. Thus the
individual plant height of the paddy varieties are lost in our effort to
obtain an overall picture.
Terms used in grouped frequency tables.
Class limits
The intervals into which the observations are put are called class
intervals. The end points of the class intervals are called
class limits. For example, the class interval 100 – 109,
has lower class limit 100 and upper class limit 109.
Class boundaries
The raw data in the above example were recorded to the nearest
centimeters. Thus, a plant height of 109.5cm would have been recorded as
110cm, a plant height of 119.4 cm would have been recorded as 119cm,
while a plant height of 119.5 cm would have been recorded as 120 cm. It
can therefore be seen that, the class interval 110 – 119, consists of
measurements greater than or equal to 109.5 cm and less than 119.5 cm.
The numbers 109.5 and 119.5 are called the lower and upper boundaries of
the class interval 110 – 120. The class boundaries of the other class
intervals are given below:
Note:
Notice that the lower class boundary of the ith class interval is the
mean of the lower class limit of the class interval and the upper class
limit of the (i-1)th class interval (i = 2, 3, 4, …). For example,
in the table above the lower class boundaries of the second and the
fourth class intervals are (110 + 119) /2 = 114.5 and (130 + 139)/2 =
134.5 respectively.
It can also be seen that the upper class boundary of the ith class
interval is the mean of the upper class limit of the class interval and
the lower class limit of the (i+1)th class interval (i = 1, 2, 3,
…). Thus, in the above table the upper class boundary of the fourth
class interval is (130 + 139)/2 = 134.5.
Class mark
The mid-point of a class interval is called the class mark or class
mid-point of the class interval. It is the average of the upper and
lower class limits of the class interval. It is also the average of the
upper and lower class boundaries of the class interval. For example, in
the table, the class mark of the third class interval was found as
follows: class mark =(120+129)/2 = (119.5 + 129.5)/2= 124.5.
Class width
The difference between the upper and lower class boundaries of a class
interval is called the class width of the class interval. Class widths
of class intervals can also be found by subtracting two consecutive
lower class limits, or by subtracting two consecutive upper class
limits.
Note:
The width of the ith class interval is the numerical difference
between the upper class limits of the ith and the ( i-1)th class
intervals (i = 2, 3, …). It is also the numerical difference between
the lower class limits of the ith and the (i+1)th class intervals (i
= 1, 2, …).
In grouped frequency table above the width of the second class interval
is |110-119| = 9. This is the numerical difference between the lower
class limits of the second and the third class intervals. The width of
the third class interval is |120-129|= 9. This is the numerical
difference between the lower class limits of the third and the fourth class intervals.
Construction of frequency distribution table
Step 1. Decide how many classes you wish to use.
Step 2. Determine the class width
Step 3. Set up the individual class limits
Step 4. Tally the items into the classes
Step 5. Count the number of items in each class
Consider the example
An agricultural student measured the lengths of leaves on an oak tree
(to the nearest cm). Measurements on 38 leaves are as follows
9,16,13,7,8,4,18,10,17,18,9,12,5,9,9,16,1,8,17,1,10,5,9,11,15,6,14,9,1,12,5,16,4,16,8,15,14,17
Step 1. Decide how many classes you wish to use.
H.A. Sturges provides a formula for determining the approximation number
of classes. \[\mathbf{k = 1 + 3.322}\mathbf{\log}\mathbf{N}\] Number of
classes should be greater than calculated k
In our example N=38, so k= (1+3.322)×log(38) = (1+3.322)×1.5797 =
6.24 = approx 7
So the approximated number of classes should be not less than 6.24
i.e.\(\ k^{'}\) =7
Step 2. Determine the class width
Generally, the class width should be the same size for all classes. C=
| max − min|/ k. Class width \(C^{'}\)should be greater than calculated
C. For this example, C = | 18− 1|/6.24 = 2.72, so
approximately class width \(C^{'} =\) 3 (Note that k used here is the
calculated value using Sturges formula not the approximated).
Step 3. To set up the individual class limits, we need to find the
lower limit only
\[L = min - \frac{C^{'} \times k^{'} - (max - min)}{2}\]
where C and k here are final approximated class width and number of
classes respectively in our example
\(L = 1 - \frac{(3 \times 7) - (18 - 1)}{2}\)=1-2=-1; since there is no
negative values in data = 0.
|
Class
|
Frequency
|
|
0-3
|
3
|
|
3-6
|
5
|
|
6-9
|
5
|
|
9-12
|
9
|
|
12-15
|
5
|
|
15-18
|
9
|
|
18-21
|
2
|
Even though the student only measured in whole numbers, the data is
continuous, so “4 cm” means the actual value could have been anywhere
from 3.5 cm to 4.5 cm.
Cumulative frequency
In many situations, we are not interested in the number of observations
in a given class interval, but in the number of observations which are
less than (or greater than) a specified value. For example, in the above
table, it can be seen that 3 leaves have length less than 3.5 cm and 9
leaves (i.e. 3 + 6) have length less than 6.5 cm. These frequencies are
called cumulative frequencies. A table of such cumulative frequencies is
called a cumulative frequency table or cumulative frequency
distribution.
Cumulative frequency is defined as a running total of frequencies.
Cumulative frequency can also defined as the sum of all previous
frequencies up to the current point. Notice that the last cumulative
frequency is equal to the sum of all the frequencies. Two types of
cumulative frequencies are Less than cumulative frequency and Greater
than cumulative frequency. Less than cumulative frequency (LCF) is the
number of values less than a specified value. Greater than cumulative
frequency (GCF) is the number of observations greater than a specified
value.
The specified value for LCF in the case of grouped frequency
distribution will be upper limits and for GCF will be the lower limits
of the classes. LCF’s are obtained by adding frequencies in the
successive classes and GCF are obtained by subtracting the successive
class frequencies from the total frequency.
Relative frequency
It is sometimes useful to know the proportion, rather than the number,
of values falling within a particular class interval. We obtain this
information by dividing the frequency of the particular class interval
by the total number of observations. Relative frequency of a class
is the frequency of class divided by total observations. Relative
frequencies all add up to 1.
|
Class
|
Frequency
|
A
|
B
|
C
|
|
0.5 - 3.5
|
3
|
3
|
38
|
0.078947
|
|
3.5 - 6.5
|
6
|
9
|
35
|
0.157895
|
|
6.5 - 9.5
|
10
|
19
|
29
|
0.263158
|
|
9.5 - 12.5
|
5
|
24
|
19
|
0.131579
|
|
12.5 - 15.5
|
5
|
29
|
14
|
0.131579
|
|
15.5 - 18.5
|
9
|
38
|
9
|
0.236842
|
[1] “Note: A= Less than cumulative frequency; B= Greater than cumulative frequency, C = Relative frequency”
“Data is the sword of the 21st century, those who wield it
well, the Samurai.” - Jonathan Rosenberg, former Google SVP