12 Sample Survey
Sample surveys are widely used as a means of collecting information to meet a definite need for the Government, Trade or industry, Science and Technology or for various activities of the society on Social, Educational or Economic problems.
Some specific situations in which the sample surveys are employed:
- When results are required with maximum accuracy (or reliability) with a fixed budget and enumerating minimum number of units.
- When the units under the investigation show considerable variation for a characteristic under study.
- When a total count of the population is not possible, or method of measurement needs destruction.
- When the scope of the investigation is very wide and the population is not completely known.
- When time money and other resources are limited.
12.1 Definition of some common terms used in sampling
Population: A group of individuals or (units) defined according to a survey. It is the collection of units of the same kind about which information is to be collected. All cultivated fields under a specified crop in an area, the population of a country, the households in a village for measuring income etc. are examples.
Sample: It is a part of the aggregate (or whole population). Inference is drawn on the basis of results obtained from a sample.
Census: It is complete enumeration of the population.
Sampling units: It is the ultimate unit from which data were collected.
Sample size: The number of units included in a sample.
Sampling designs or sampling methods: A scientific and objective procedure of selecting units from a population and getting a sample that is expected to be representative of the whole population. It provides procedures for the estimation of results that would be obtained if a comparable survey was taken on all the units of the population.
Parameters and statistics: The statistical measures of the population like mean, variance etc. is referred to as parameters. The statistical measures computed from sample observations are called Statistics.
Expectation: It is the arithmetic mean of all possible values of the statistic expressed as E(statistic) = Expected value or expectation of a statistic
Unbiased estimate: A statistic t(a function of the sample values) is an unbiased estimate of the population parameter say θ if the Expectation of t = θ ie., E(Statistic) = Parameter.
Sampling error: A sample survey can never reproduce exactly the various characteristics of the population (unless the population itself is surveyed and a census is conducted). The discrepancy between sample estimates and the population values (obtained by estimating all the units) are termed as sampling error.
As long as the sampling errors are sufficiently small, the sampling method can be adopted for studying a population. Sampling errors are absent in complete enumeration.
It is primarily due to (i) faulty selection of samples (ii) substitution of sampling units which are already included in a study. (iii) faulty demarcation of sampling units. (iv) and constant errors due to improper choice of Statistical methods for the estimation of parameters.
Increasing the sample size decreases the sampling error.
Non sampling error: Errors other than sampling errors such as those arising through non response, incompleteness, inaccuracy, etc. are called non sampling errors. The data obtained from a census is free from sampling errors but still it is subjected to non sampling errors. (Sample survey data are subjected to both these errors.)
The non sampling errors can occur due to (i) Faulty planning and faulty definitions – inadequate data specifications, errors in locating the units, lack of trained persons etc. (ii) Response errors- misunderstanding a question, bias of interviewer or respondent (iii) Non response bias – full information is not obtained/collected. (iv) Errors in coverage and compilation and publication errors.
12.2 Sample Suervey-Methods
Principal steps in a sample survey:
- Decide the objectives of the survey.
- Define the population to be surveyed.
- The frame and sampling units (The population can be divided into sampling units which cover the entire population and they must be distinct, unambiguous and non-overlapping. The list, map or other material covering the population is called a frame.)
- Identify the data to be collected.
- Preparation of questionnaire or schedule.
- Decide method of collecting information (interview, mailing etc.)
- Procedures for non respondents.
- Selection of proper sampling designs for a desired degree of precision.
- Organization of field work.
- The pre tests
- Summary and analysis of data (scrutinizing, editing tabulating etc.)
- Record the information gained for future surveys.
12.3 Methods of Sampling
The various methods of sampling can be grouped under
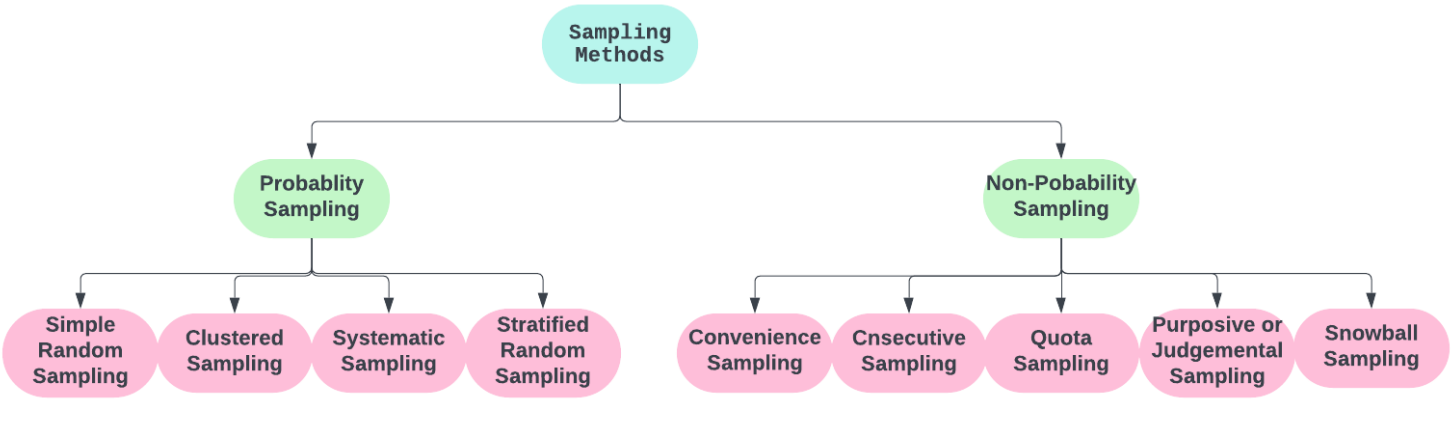
Figure 12.1: Sampling methods classification
12.3.1 Probability sampling:
Probability sampling is the scientific method of selecting samples according to some laws of chance in which each unit in the population has some definite pre assigned probability of being selected in the sample like:
- Units have an equal chance of being chosen.
- Sometimes units are selected with different probabilities.
- Probability of selection is proportional to size of the units.
12.3.1.1 Simple Random Sampling
This is the fundamental and simple method of drawing probability samples. It is used when all the population units are nearly homogeneous with respect to the study variables. The units can be selected with or without replacement methods. When a number (unit) drawn is removed from the population for all subsequent draws this method is called Simple random sampling (SRS) without replacement.
In simple random sample of size n with replacement, all possible samples of size n have equal chance to be selected for the survey. Units are numbered from 1, 2,…,N and n numbers are drawn one by one by assigning equal probability of selection to each of the units in the first and subsequent draws. The samples can be drawn at random either by lottery method or by using random numbers.
Let there be N population units and n be the sample size to be selected. Simple random sampling is a method of selecting n units such that every one of the distinct samples has an equal chance of being drawn.
Example: Suppose we want to select a simple random sample of 100 students from a college. Here, we can assign a number to every student in the college database from 1 to 300 and use a random number generator to select a sample of 100 numbers.
12.3.1.2 Stratified random sampling
A stratified sampling approach divides the entire population into smaller groups to complete the sampling procedure. The small group is generated based on a few demographic parameters. After dividing the population into smaller groups, statisticians draw a random sample.
Example: There are three boxes (A, B and C), each with different balls. Bag A has 100 balls, bag B has 150 balls, and bag C has 200 balls. We have to choose a sample of balls from each bag proportionally. Suppose 1 balls from bag A, 10 balls from bag B and 20 balls from bag C.
12.3.1.3 Systematic sampling
The systematic sampling method selects items from the target population by selecting a random selection point and then selecting the other methods after a predetermined sample interval. It is determined by dividing the total population size by the target population size.
Example: Suppose the names of 300 graduates of a college are sorted in the reverse alphabetical order. To select a sample in a systematic sampling method, we have to choose some 15 graduates by randomly selecting a starting number, say 5. From number 5 onwards, will select every 15th person from the sorted list. Finally, we can end up with a sample of some graduates.
12.3.1.4 Cluster sampling
The clustered sampling method creates a cluster or group of objects from the population set. The group shares comparable significatory traits. Also, they have an equal chance of being included in the sample. This method use basic random sampling for the cluster of population.
Example: The list of all the agricultural fields in a village or a district may not be easily available but the list of village or districts are generally available. In this case, every farm in sampling unit and every village or district is the cluster. Draw a sample of clusters from villages and then collect the observations on all the sampling units available in the selected clusters.
12.3.2 Non-probability sampling
The non-probability sampling method is one in which the researcher chooses a sample based on subjective judgement rather than random selection. This approach excludes some population members from getting involved with the study.
12.3.2.1 Convenience sampling
Convenience sampling is probably the most effective type of non-probability sampling. Researchers select members based on their accessibility and closeness, making it easier to collect data.The samples are easy to select, and the researcher did not choose the sample that outlines the entire population.
Example: Surveying peoples at a shopping center or a nearby park would be considered a convenience pattern.
12.3.2.2 Consecutive sampling
Consecutive sampling is similar to convenience sampling with a minor difference. Here, the researcher chooses a sample or group of people, conducts study over time, collects data, and then moves on to the next sample.
Example: When companies/ brands stop people in a crowded areas and hand them promotional leaflets to purchase a luxury car.
12.3.2.3 Quota sampling
Quota sampling divides the population into subgroups or strata and assigns a quota to each grouping. Researchers collect data from individuals within each subgroup until the quota is satisfied. While it allows for stratification, it does not guarantee accuracy and may result in selection bias if quotas are not carefully designed.
Example: In a marketplace studies have a look at for a new cosmetic product, the studies team makes a decision to accumulate facts from customers at a nearby beauty store. They divide capacity contributors into classes based totally on demographics, such as age and gender. For each category, they set a selected quota, like 40 girls elderly 20-30 and 20 men aged 25-35, and so on. The researchers then approach shoppers within the mall till they’ve filled every quota. Quota sampling lets in for a sure stage of stratification but does not contain random choice, as contributors are decided on to fill predefined quotas.
12.3.2.4 Purposive sampling
In this sampling, researchers select persons who they believe are most applicable or familiar with the study topic. This strategy is widely used in qualitative research or when specialist evaluations are necessary. However, it can introduce researcher bias and may not be suitable for generalisation. It is also known as judgmental sampling.
Example: A researcher is conducting a study on the performance of top-performing farmer in a big village. Instead of choosing farmer randomly, the researcher chooses to review farmer who have acquired a couple of awards and recognitions for their terrific work. This is an example of judgmental or purposive sampling, in which the researcher deliberately selects contributors who are taken into consideration expert or have precise characteristics relevant to the research topic.
12.3.2.5 Snowball sampling
Snowball sampling is also known as a chain-referral sampling method. It is usually used while the target population is hard to reach, which include hidden or marginalized communities.So, each recognised member of a population is asked to locate the remaining sampling units. Those sampling units are also from the same target population.
Example: Consider a study aiming at understanding the experiences of illegal immigrants in a certain city. Given the hidden and frequently marginalised nature of this population, the researcher starts by identifying and interviewing one undocumented immigrant. Following the interview, the researcher requests that the initial participant suggest them to others who are likely willing to participate in the research. This process continues with each player referring the researcher to more capable individuals.
Limitations of Sampling methods:
- Sometimes samples do not fully cover the population and consequently the results are not exact.
- Sampling theory is not dependable unless trained and qualified persons were employed in the field.
- The planning and execution should be done carefully or the data may provide misleading results.